If less is more, is “lesson” the opposite of “moron”, or is it even more stupid?
More Chords
Forget all about which hand is most artisty — today it’s all about chords.
So far, we’ve covered most of the “simple” chords. Here are the ones that are left:
o oo o o oo o oooo ====== ====== ====== |||1|| |||1|| |||||| ------ ------ ------ |23||| |2|||| |2|||| ------ ------ ------ |||||| |||||| |||||| ------ ------ ------ E E7 Em7 ooo x 0 x o ====== ====== ====== |||||1 ||1||| ||||1| ------ ------ ------ |2|||| |2|3|4 ||2||| ------ ------ ------ 3||||| |||||| |3|4|| ------ ------ ------ G7 B7 C7 x o x o x o ====== ====== ====== |||||1 ||||11 ||||1| ------ ------ ------ |||2|| |||2|| |||2|3 ------ ------ ------ ||||3| |||||| |||||| ------ ------ ------ Dm Dm7 D7
With these chords under your belt, plus the ones we’ve already covered, you should be able to play a large amount of the songs you will find on dylanchords or any other chordsite. The exceptions are songs with barre chords and songs with chords with long and complicated names, which will the topics of later lessons.
For now, just a few remarks on the most common chords.
- G7: Note the similarity between G7 and C: the pattern is the same, only with the chord “spread out” on all six strings. Take advantage of this wen you play these chords and keep the movement as simple as possible.
- E is the quintessential blues chord. Most of John Lee Hooker’s songs and a good share of the blues songs you will hear in pub bands are in this key. Its companion chords are A and B7. With those three chords, you can pick more or less any blues song and play it, and that is the first assignment today: pick any blues song and play it.
- B7 is one of those four-finger chords, which may seem difficult to get in place all at the same time. It should work as a block of fingers, as I’ve talked about before — not as four separate fingers. This could be trained in the usual way: play E – B7 – E – B7 for two minutes, and chances are that you will come out with a fairly automatized B7. Again: the long finger is in the same place in the two chords. Use that as a stabilizing element.
It is possible to cheat with B7 and play it x21200 instead, which — if you come from E — is just a matter of switching strings for the index and ring fingers. The “wrong” tone you will be playing is the high e’, and since you will most likely play B7 only in songs in E major, that is either completely wrong — if the “point” of the song is maximum contrast between the two — or completely ok. You decide — it’s your ears.
In the more advanced direction, it is also possible to get a finger at the second fret of the sixth string as well, somehow: 221202. This would either be a half-barre with the longfinger, covering both the fifth and the sixth strings, or a thumb coming up from behind to the sixth string. I will come back to both these solutions later. For now, you’re probably better off cheating (I do that, most of the time…). - Dm is one of those spread-out chords, which may give some problems until you get used to stretching out your hand.
- C: The common C major chord can be played in four different ways:
x o o ====== ||||1| ------ ||2||| ------ |3|||| o o x o x o ====== ====== ====== ||||1| ||||1| ||||1| ------ ------ ------ ||2||| ||2||| ||2||| ------ ------ ------ 34|||| |3|||4 3||||4 variants of CThe shape at the top is the one we have used so far. It is the easiest one, at least insofar as it only uses three fingers, but I recommend learning the other three as well.
The first (332010) is my everyday C. It has two great advantages: (1) it makes the sixth string less obtrusive, so you can actually play the chord with the full six strings; and (2) it works perfectly together with the version of G major with long, ring and little fingers that I recommended back in lesson 3: the ring finger is already in place (“already in place” is a thing to look for, especially when it’s the ring finger, the least mobile of the fingers), the long finger is almost there, and it’s a relatively small matter to slip the little finger down to the first string.
Apropos — in the version in the middle (x32013) the little finger is already in place on the first string, and all you need to do to get to G is slip the little and ring fingers up to the fifth and sixth strings and let go of the index finger. The little finger on the first string gives this chord shape a very distinct sound: one high tone is ringing way above the next one. This makes it a nice variant, but it can also be too much sometimes. Use it with care.
The last variant is a special chord, to be used in one specific context:ooo x o ooo ====== ====== ====== |||||| ||||1| |||||| ------ ------ ------ |2|||| -> ||2||| -> |2|||| ------ ------ ------ 3||||4 3||||4 3||||4 G C/g G
Here, two fingers are “already in place”, and slipping the long finger one string down and adding the index finger is easy enough. This is one of the cases where you are supposed to touch a neighbouring string: the fifth string should not sound, and muting it is the job of the ring finger. It happens almost automatically.
The “C character” of the C major chord suffers here, since the bass tone is G and the fifth string should not be sounding. It is, in other words, a variant chord to G almost as much as a proper C chord. - G: I’ve said it before, but for the sake of completeness: try to learn to play G with the “bad” fingers — you will not regret it.
Overtones and sound quality
A few more words about the E major chord:
E is the biggest, fattest chord in the book. Since E is the tone of the deepest string, it follows that E is the deepest sounding chord you can play in standard tuning. But that’s not the only reason; there are things about the way the chord is constructed which emphasise this grandness.
Try this: Play the open 6th string. Then place your finger over the twelfth fret (and when I say “over” I mean that literally: directly over the metal band and not “in the box” where you will usually place your fingers), and touch the string lightly but without pressing down on the string. Then strike the string again. You should hear the same tone as the open string, only an octave higher, and with a somewhat flute-like sound (at least that’s what those people thought it sounded like who called this kind of tones “flageolets”, which means “little flutes”).
Do the same thing again, this time touching the string over the seventh fret, then over the fifth fret. The fifth-fret tone should be the same tone again, another octave higher. This should be the same tone as the open first string. The seventh-fret tone, on the other hand, is not an e, but a b, which should sound the same as the open second string.
What you have just played, are the first three overtones or harmonics of the tone E. When you strike a string, you are setting the string in vibration. But it’s not just the whole string that is vibrating. The two halves of the string are also vibrating, independently of what’s happening with the full string. So are the three thirds of the string, etc.
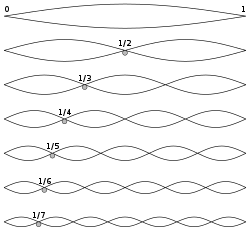
What you are doing when you touch the string at the twelfth fret, is partly to stop the full vibration of the string, partly to emphasise the vibrations of the two halves of the string. The twelfth fret is the exact middle of the string, corresponding to the point marked “1/2” in the image to the right.
Similarly, the seventh fret marks one third of the string (“1/3” in the figure), and the fifth fret one fourth, etc. There are similar points at the fourth fret, near the third fret, etc. In principle, the series does not end, but it is difficult to isolate the higher overtones in practice.
They are there, however, and they are heard. The combination of overtones — which ones are more and which less loud — is one of the most important factors that determine how an instrument sounds. A violin has a different distribution of overtones than a guitar, and that’s why we can hear the difference between them. (The other main elements are the attack — how the tone starts — and the sustain — how it ends. If one cuts off the attack, it can be surprisingly difficult to recognize an instrument sound.)
But even one and the same instrument can have different sounds. If you strike a string close to the bridge, it sounds much sharper than if you strike it closer to the sound hole: you are in fact emphasising the higher overtones, whereas closer to the sound hole, you’re giving more punch to the lower ones, which gives a darker, mellower sound.
We can now go back to the E major chord, and summarize what we know: when we strike the deepest string, we also hear — among the overtones of that tone — three tones that are also part of the full chord, on different strings: the fourth, second and first strings are identical to the first, second and third overtones, respectively. The tone on the fifth string (B) does not correspond directly to any of the overtones, but it is at least the same tone as the second string, an octave lower, and will feel very much at home in the chord.
In other words: most of the tones in the E major chord are there already in the deepest-sounding tone. The rest of the strings reinforce the basic sound. Hence the full, rich sound of the chord as a whole.
The third
That leaves one string: the third. The tone of the third string is g# (g sharp), which is the third of the E major chord — the tone which decides if the chord is major or minor. Its position right in the middle of the chord is ideal: it does not draw too much attention to itself (as may be the case with D major, where the third (f#) is played on the first string), nor does it blur the chord (as may be the case if the third is placed closer to the bass).
The third is the unruly pubescent teenager in the family of chords: it certainly has character, and the chord would be a whole less interesting without it, but somehow, it is always either too big or too small.
This is not just metaphorically speaking: it is too big or too small. Or put differently: a third on the guitar will always be out of tune. This has to do with properties of the tonal system, which it will take to long to give the details about, but to make it brief: the fourth overtone (the one on the fourth fret) is two octaves and a third above the tone of the open string. This tone or one equal to it will sound in tune with the fundamental tone. The problem is that this tone can not be produced in a system which is based on a division of the octave into twelve equal (or rather: proportionally equidistant) tones, which is how the guitar is constructed, with twelve equal frets on an octave. This is also how modern pianos are tuned. The benefit of this system — which Johann Sebastian Bach demonstrated with his Well-Tempered Klavier — is that one can play equally well in any possible key. The cost is that every interval except the octave is slightly out of tune. With some intervals, it is hardly noticeable, but with the third, the difference between the pure and the tempered version is considerable.
You can test this by playing the fourth fret flageolet on the sixth string and comparing it with the tone on the fourth fret of the first string (g sharp). If the two strings are perfectly in tune, you should be able to hear the difference between the two tones clearly: the pure third, on the sixth string, is consideably smaller than the one you play on the first string.
This is yet another reason why the third in a chord should be treated with caution — just like with a teenager. In the middle, surrounded by caring and loving octaves and fifths — as it is in E major — it blends in more easily, but if it is allowed to ring all by itself on the top (as in D major), it can be jarring at worst (and interesting at best…).
*
My plan was to say something more about the blues today, but on second thought, I think I will leave it to the lesson on licks and riffs — after all, that’s mainly what the blues is all about.
All the Lessons
[catlist name=Lessons numberposts=150 order=asc orderby=date excludeposts=419]

Leave a Reply